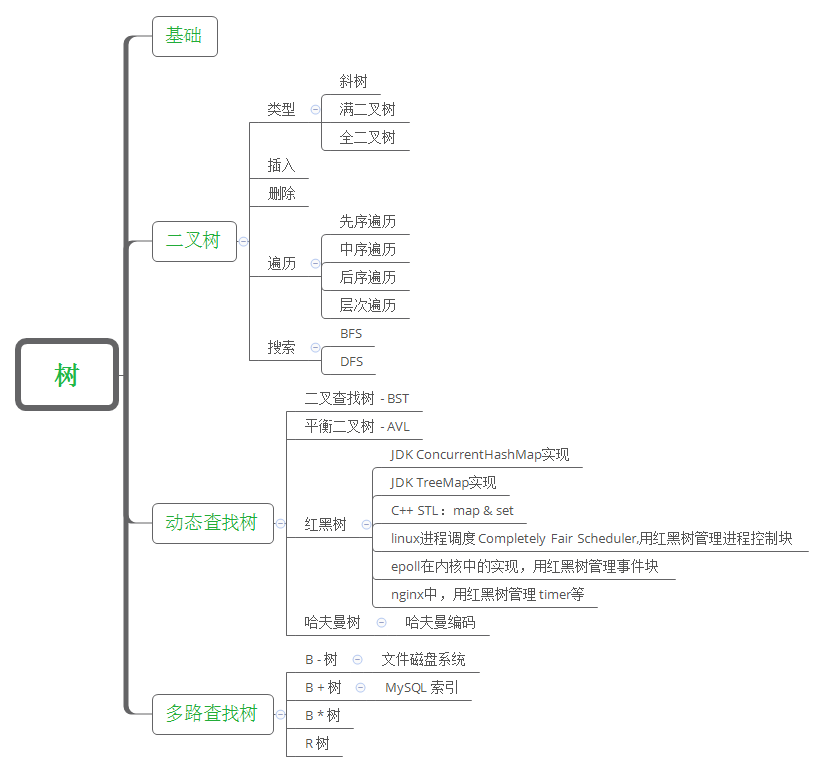
• 二叉树
  • 动态查找树
    1. 二叉查找树 BST
    2. 平衡二叉树 AVL
    3. 红黑树 RBT
    4. 哈夫曼树
  • 多路查找树
    1. B树
    2. B+树
    3. R树

1.二分搜索树（BST）

二叉树——>完全二叉树——>满二叉树
二叉树具有天然递归结构：每个节点的左子树也是二叉树，每个节点的右子树也是二叉树。

二分搜索树的每个节点的值

大于其左子树的所有节点的值，小于其右子树的所有节点的值。
二分搜索树中存储的元素必须有可比较性。

二分搜索树的前中后序遍历

2.平衡二叉树(AVL)

基于BST存在的问题，一种新的树——平衡二叉查找树(Balanced BST)产生了。平衡树在插入和删除的时候，会通过旋转操作将高度保持在logN。其中两款具有代表性的平衡树分别为AVL树和红黑树。AVL树由于实现比较复杂，而且插入和删除性能差，在实际环境下的应用不如红黑树。

AVL树的应用场景：

  • windows对进程地址空间的管理

3.红黑树（R-B Tree）

  1. 任何一个节点都有颜色，黑色或者红色。
  2. 根节点是黑色的。
  3. 父子节点之间不能出现两个连续的红节点。
  4. 任何一个节点向下遍历到其子孙的叶子节点，所经过的黑节点个数必须相等。
  5. 空节点被认为是黑色的。

红黑树的应用场景：

  1. epoll在内核中的实现，用红黑树管理事件块（文件描述符）
  2. Java的TreeMap实现
  3. nginx中，用红黑树管理timer
  4. linux进程调度Completely Fair Scheduler,用红黑树管理进程控制块

4.B-树

B-树是一种多路平衡查找树，在文件系统中很有用。
一颗m阶的B-树，或为空树，或为满足下列特性的m叉树：
1)树中每个节点至多有m棵子树；
2)若根节点不是叶子节点，则至少有两棵子树；
3)除根之外的所有非终端节点至少有m/2上限棵子树；
4)所有的非终端节点中包含下列信息数据：(n，A0，K1，A1，K2，A2，……，Kn，An)。其中，n(m/2-1<=n<=m-1)为关键字的个数(或n+1为该节点子树的个数)；Ki(1<=i<=n)为关键字，且Ki< Ki+1；Ai(0<=i<=n)为指向该节点子树根节点的指针，且指针Ai-1所指子树中所有节点的关键字均小于Ki，An所指子树中所有的节点的关键字均大于Kn。
5)所有叶子结点位于同一层。保证平衡。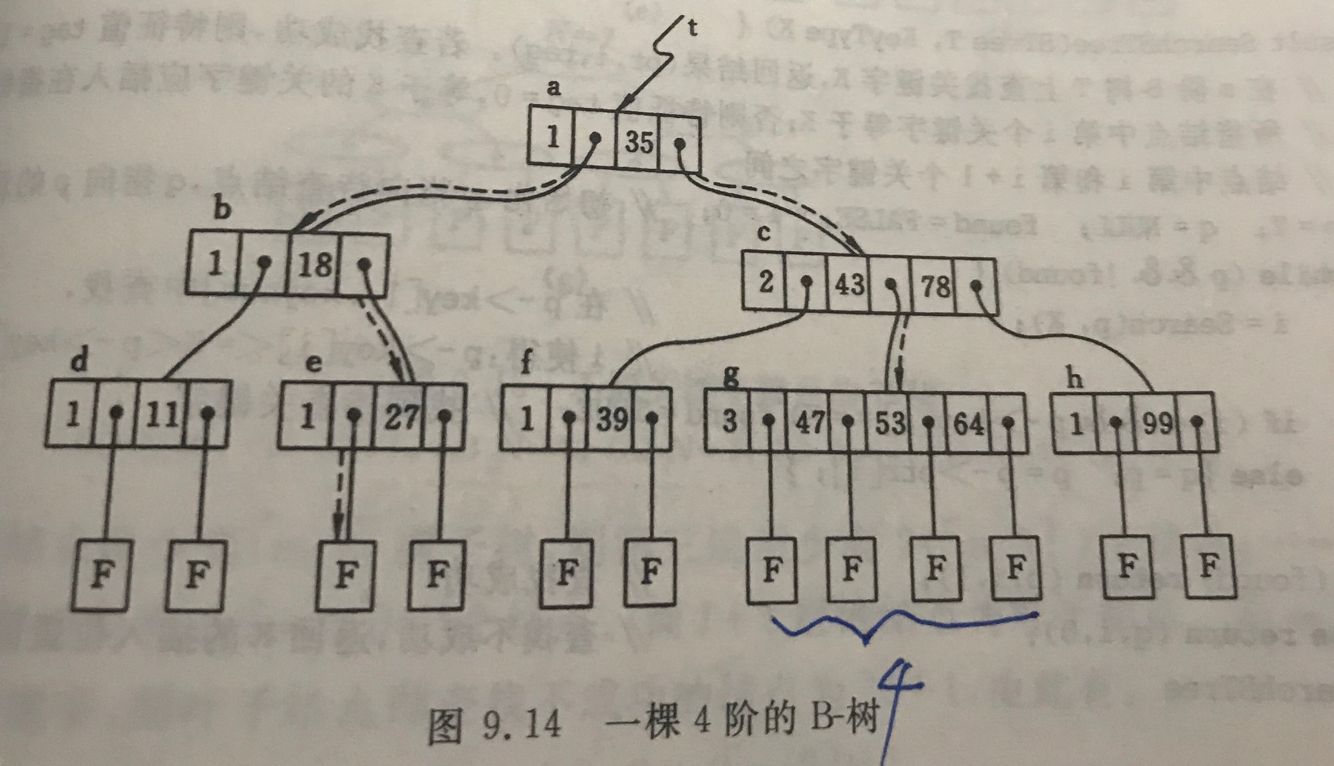

B树的查找

在B-树上进行查找的过程是一个顺指针查找结点和在结点的关键字中进行查找交叉进行的过程。
由于B-树用作文件的索引，因此它的查找涉及外存的存取。
在B-树上进行查找包含两种操作：(1)在B-树中找节点；(2)在节点中找关键字。由于B-树通常存储在磁盘上，则前一查找操作是在磁盘上进行的，而后一查找操作实在内存中进行的，即在磁盘上找到指针p所指节点后，先将节点中的信息读入内存，然后再利用顺序查找或折半查找查询等于K的关键字。

B树的插入

插入和分裂
m阶的B树，每个结点最多m-1个关键字，保证最多有m棵子树。

B树的删除

B树怎么保证绝对平衡的？

5.B+树

B+树是应文件系统所需而出的一种B-树的变型树(严格来说，它已不是此前定义的树了)。
一棵m阶的B+树和m阶的B-树的差异在于：
1)有n棵子树的节点中含有n个关键字；
2)所有的叶子节点中包含了全部关键字的信息，及指向含这些关键字记录的指针，且叶子节点本身依关键字的大小自小而大顺序链接；
3)所有的非终端节点可以看成是索引部分，节点中仅含有其子树(根节点)中的最大(或最小)关键字。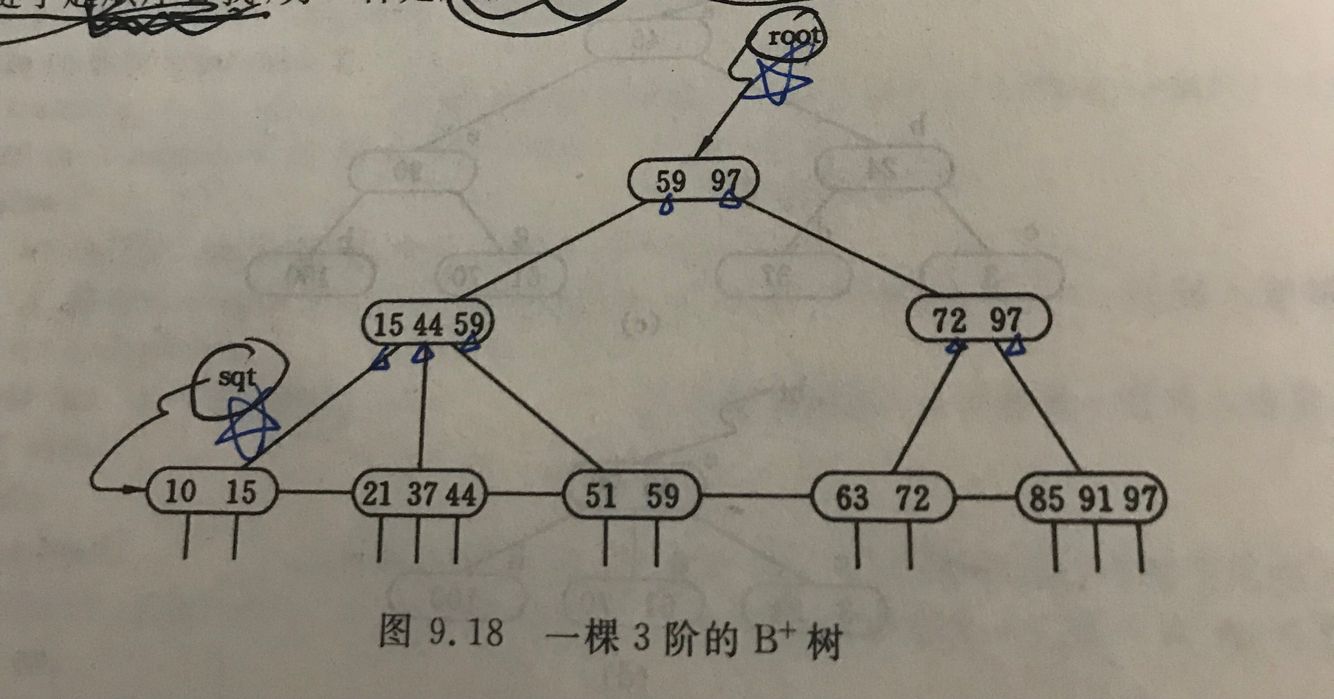

B+树的查找

B+树的插入

B+树的插入仅在叶子节点上进行，当节点中的关键字个数大于m时要分裂成两个节点，它们所含关键字的个数分别为(m+1)/2的上界，并且它们的双亲结点中应同时包含这两个结点中的最大关键字。

B+树的删除

B+树的删除也仅在叶子节点进行，当叶子结点中的最大关键字被删除时，其在非终端结点中的值可以作为一个“分界关键字”存在。若因删除而使节点中关键字的个数少于m/2时，其和兄弟节点的合并过程和B-树类似。

6.线段树(区间树)

线段树不是完全二叉树，是平衡二叉树。