冒泡排序

算法描述：将第一个记录的关键字和第二个记录的关键字进行比较，若为逆序（即L.r[1].key>L.r[2].key），则将两个记录交换之，然后比较第二个记录和第三个记录。依次类推，直到第n-1个记录和第n个记录的关键字进行过比较为止，此过程称为第一趟起泡排序，其结果使得关键字最大的记录被安置到最后一个记录的位置上。最坏情况，初始序列为“逆序”，需进行n-1趟排序，进行n(n-1)/2次比较，并做等数量级的记录移动，时间复杂度为O(n的平方)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public class BubbleSort {

    public static void bubbleSore(int[] arr) {
        int len = arr.length;

        for (int i = 0; i < len - 1; i ++) {
            boolean flag = true;
            for (int j = 0; j < len - 1 - i; j ++){
                // 前者大于后者 交换之
                if (arr[j] > arr[j + 1]) {
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                    flag = false;
                }
            }
            // 节省最后几趟过程，前面的元素可能已经有序了
            if (flag) {
                break;
            }
        }
    }

    public static void main(String[] args) {
        int[] arr = new int[]{11,25,4,999,3,1};
        bubbleSore(arr);
        System.out.println(Arrays.toString(arr));
    }
}

快速排序

快速排序是对冒泡排序的一种改进。它的基本思想是，通过一趟排序将待排记录分割成独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。
一趟快速排序的具体做法是：附设两个指针low和high，它们的初值分别为low和high，设枢轴记录的关键字为pivotkey，则首先从high所指位置起向前搜索找到第一个关键字小于pivotkey的记录和枢轴记录互相交换，然后从low所指位置起向后搜索，找到第一个关键字大于pivotkey的记录和枢轴记录互相交换，重复这两步直至low=high为止。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
//java实现
public static void quickSort(int[] a,int low,int high){
    int pivot;
    if(low < high) {
        pivot = partition(a, low, high);
        quickSort(a, low, pivot-1);
        quickSort(a, pivot+1, high);
    }
}
public static int partition(int[] a, int first, int end) {
    int i=first;
    int j=end;
    while(i < j) {
        while(i < j && a[i] <= a[j]) {  //右侧扫描
            j--;
        }
        if(i < j) {  //将较小记录交换到前面
            int temp = a[i];
            a[i] = a[j];
            a[j] = temp;
            //i++;
        } 
        while(i < j && a[i] <= a[j]) { //左侧扫描
            i++;
        }
        if(i < j) { //将较大记录交换到后面
            int temp = a[i];
            a[i] = a[j];
            a[j] = temp;
            //j--;
        }
    }
    return i;
}

选择排序——简单选择排序

算法描述：对于给定的一组记录，经过第一轮比较后得到最小的记录，然后将该记录与第一个记录的位置进行交换，接着对不包括第一个记录以外的其他记录进行第二轮比较，得到最小的记录并与第二个记录进行位置交换，重复该过程，直到进行比较的记录只有一个时为止。
选择排序每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/**
 * 选择排序
 * 平均O(n^2),最好O(n^2),最坏O(n^2);空间复杂度O(1);不稳定;简单
 */
public class SelectionSort {
 
    public static void selectionSort(int[] arr) {
        int n = arr.length;
        for (int i = 0; i < n; i++) {
            int k = i;
            // 找出最小值的下标
            for (int j = i + 1; j < n; j++) {
                if (arr[j] < arr[k]) {
                    k = j;
                }
            }
            // 将最小值放到未排序记录的第一个位置
            if (k > i) {
                int tmp = arr[i];
                arr[i] = arr[k];
                arr[k] = tmp;
            }
        }

        int len = n;

        for(int i = 0; i < len-1; i++) {
            for(int j = i+1; j < len; j++) {
                if(arr[i] > arr[j]) {
                    int temp = arr[i];
                    arr[i] = arr[j];
                    arr[j] = temp;
                }
            }
        }
    }
 
    public static void main(String[] args) {
        int[] b = { 49, 38, 65, 97, 76, 13, 27, 50 };
        selectionSort(b);
        for (int i : b)
            System.out.print(i + " ");
    }
}

插入排序

将数组中的数据分为两个区间，已排序区间和未排序区间。初始已排序区间只有一个元素，就是数组的第一个元素。插入算法的核心思想是取未排序区间中的元素，在已排序区间中找到合适的插入位置将其插入，并保证已排序区间数据一致有序。重复这个过程，直到未排序区间中元素为空，算法结束。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
//a表示数组 n表示数组长度
public void insertSort(int[] arr,int n){
    if(n <= 1) return;

    for(int i = 1; i < n; i++){
        int value = arr[i];
        int j = i - 1;
        //查找插入的位置
        for(;j >= 0; j--){
            if(arr[j] > value){
                arr[j+1] = arr[j]; //数据移动
            }else {
                break;
            }
        }
        arr[j+1] = value;
    }

    for(int i = 1; i < n; i++) {
        for(int j = i-1; j >= 0; j--) {
            if(arr[j+1] < arr[j]) {
                int temp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = temp;
            }else {
                break;
            }
        }
    }
}

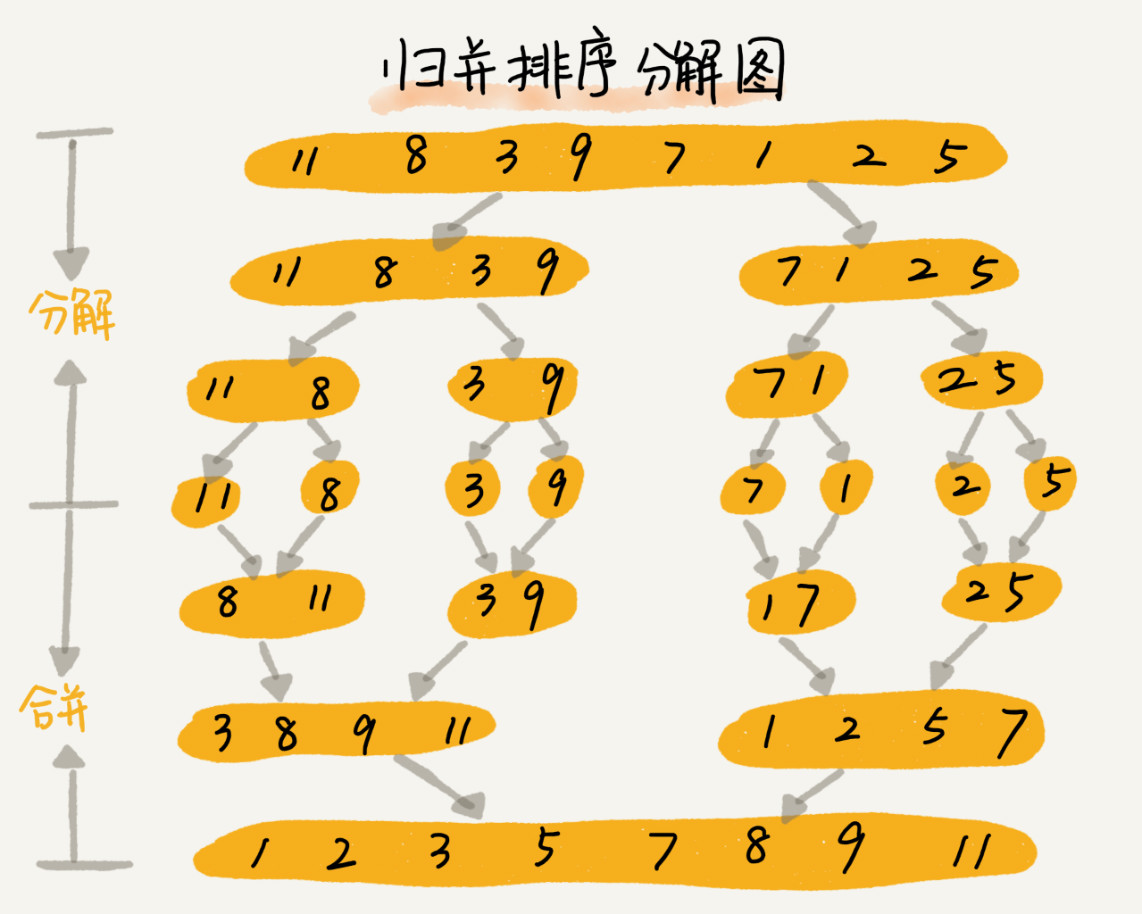
选择排序——堆排序

希尔排序

归并排序

思想：要排序一个数组，先把数组从中间分成前后两部分，然后对前后两部分分别排序，再将排好序的两部分合并在一起，这样整个数组就都有序了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
public class MergeSort {

  // 归并排序算法, a是数组，n表示数组大小
  public static void mergeSort(int[] a, int n) {
    mergeSortInternally(a, 0, n-1);
  }

  // 递归调用函数
  private static void mergeSortInternally(int[] a, int p, int r) {
    // 递归终止条件
    if (p >= r) return;

    // 取p到r之间的中间位置q,防止（p+r）的和超过int类型最大值
    int q = p + (r - p)/2;
    // 分治递归
    mergeSortInternally(a, p, q);
    mergeSortInternally(a, q+1, r);

    // 将A[p...q]和A[q+1...r]合并为A[p...r]
    merge(a, p, q, r);
  }

  private static void merge(int[] a, int p, int q, int r) {
    int i = p;
    int j = q+1;
    int k = 0; // 初始化变量i, j, k
    int[] tmp = new int[r-p+1]; // 申请一个大小跟a[p...r]一样的临时数组
    while (i<=q && j<=r) {
      if (a[i] <= a[j]) {
        tmp[k++] = a[i++]; // i++等于i:=i+1
      } else {
        tmp[k++] = a[j++];
      }
    }

    // 判断哪个子数组中有剩余的数据
    int start = i;
    int end = q;
    if (j <= r) {
      start = j;
      end = r;
    }

    // 将剩余的数据拷贝到临时数组tmp
    while (start <= end) {
      tmp[k++] = a[start++];
    }

    // 将tmp中的数组拷贝回a[p...r]
    for (i = 0; i <= r-p; ++i) {
      a[p+i] = tmp[i];
    }
  }

}

基数排序

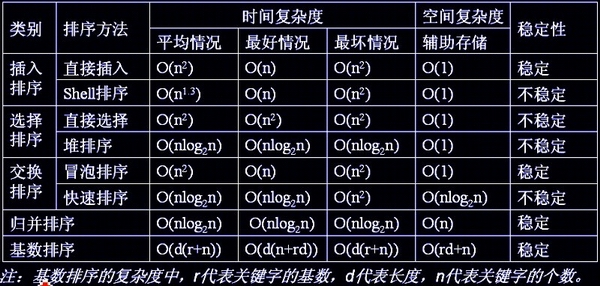
复杂度总结

复杂度总结