数据结构与算法——栈

思考：如何实现浏览器的前进和后退功能？
当你依次访问完一串页面a-b-c之后，点击浏览器的后退按钮，就可以查看之前浏览过的页面b和a。当你后退到页面a，点击前进按钮，就可以重新查看页面b和c。但是，如果你后退到页面b后，点击了新的页面d，那就无法在通过前进、后退功能查看页面c了。

如何理解栈？

关于“栈”，有一个非常贴切的例子，就是一摞叠在一起的盘子。放盘子的时候，都是从下往上一个一个放；取的时候，从上往下一个一个地依次取，不能从中间任意抽出。
后进者先出，先进者后出，这就是典型的“栈”结构。

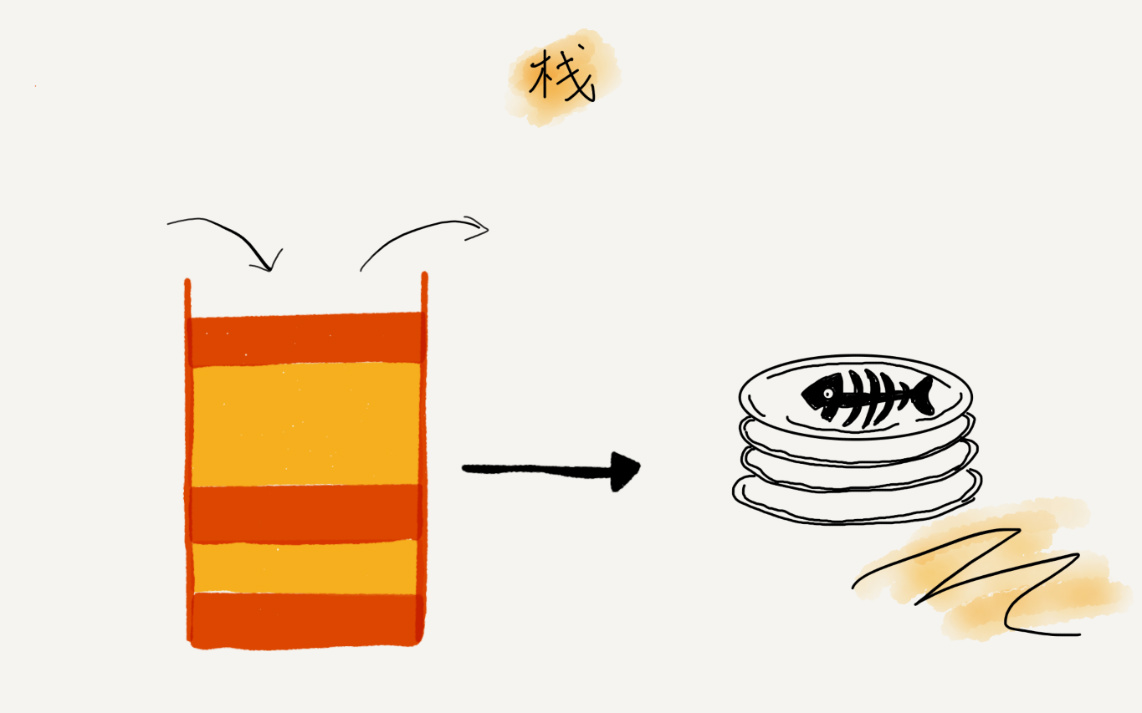
从栈的操作特性上看，栈是一种“操作受限”的线性表，只允许在一端插入和删除数据。

特定的数据结构是对特定场景的抽象。
栈与数组或链表相比，数组或链表暴露了太多的操作接口，操作上的确灵活自由，但使用时比较不可控。
当某个数据集合只涉及在一端插入和删除数据，并且满足后进先出、先进后出的特性，我们就应该首选“栈”这种数据结构。

如何实现一个“栈”？

栈主要包含两个操作，入栈和出栈，也就是在栈顶插入一个数据和从栈顶删除一个数据。
栈既可以用数组来实现，也可以用链表来实现。
用数组实现的栈，叫做顺序栈；用链表实现的栈，叫做链式栈。

数组实现

// 基于数组实现的顺序栈
public class ArrayStack {

  private String[] items;  // 数组
  private int count;       // 栈中元素个数
  private int n;           // 栈的大小

  // 初始化数组，申请一个大小为 n 的数组空间
  public ArrayStack(int n) {
    this.items = new String[n];
    this.n = n;
    this.count = 0;
  }

  // 入栈操作
  public boolean push(String item) {
    // 数组空间不够了，直接返回 false，入栈失败。
    if (count == n) return false;
    // 将 item 放到下标为 count 的位置，并且 count 加一
    items[count] = item;
    ++count;
    return true;
  }
  
  // 出栈操作
  public String pop() {
    // 栈为空，则直接返回 null
    if (count == 0) return null;
    // 返回下标为 count-1 的数组元素，并且栈中元素个数 count 减一
    String tmp = items[count-1];
    --count;
    return tmp;
  }
}

链表实现

//基于链表实现的链式栈
public class StackBasedOnLinkedList {

	private static class Node {
    private int data;
    private Node next;

    public Node(int data, Node next) {
      this.data = data;
      this.next = next;
    }

    public int getData() {
      return data;
    }
  }
  
  private Node top = null;

  public void push(int value) {
    Node newNode = new Node(value, null);

    if (top == null) {
      top = newNode;
    } else {
      newNode.next = top;
      top = newNode;
    }
  }

  public int pop() {
    if (top == null) return -1;
    int value = top.data;
    top = top.next;
    return value;
  }

  public void printAll() {
    Node p = top;
    while (p != null) {
      System.out.print(p.data + " ");
      p = p.next;
    }
    System.out.println();
  }
}

不管是顺序栈还是链式栈，我们存储数据只需要一个大小为n的数组就够了。在入栈和出栈过程中，只需要一两个临时变量存储空间，所以空间复杂度是O(1)。入栈、出栈只涉及栈顶个别数据的操作，所以时间复杂度是O(1)。
注意，这里存储数据需要一个大小为n的数组，并不是说空间复杂度就是O(n)。因为，这n个空间是必须的，无法省掉。所以在说空间复杂度的时候，是指除了原本的数据存储空间外，算法运行还需要额外的存储空间。

支持动态扩容的顺序栈

刚才那个基于数组实现的栈，是一个固定大小的栈，也就是说，在初始化栈时需要事先指定栈的大小。当栈满之后，就无法再往栈里添加数据了。
尽管链式栈的大小不受限，但要存储next指针，内存消耗相对较多。
如何基于数组实现一个可以支持动态扩容的栈呢？

基于数组实现一个可以支持动态扩容的栈，只需要底层依赖一个支持动态扩容的数组就可以了。当栈满了之后，就申请一个更大的数组，将原来的数据搬移到新数组中。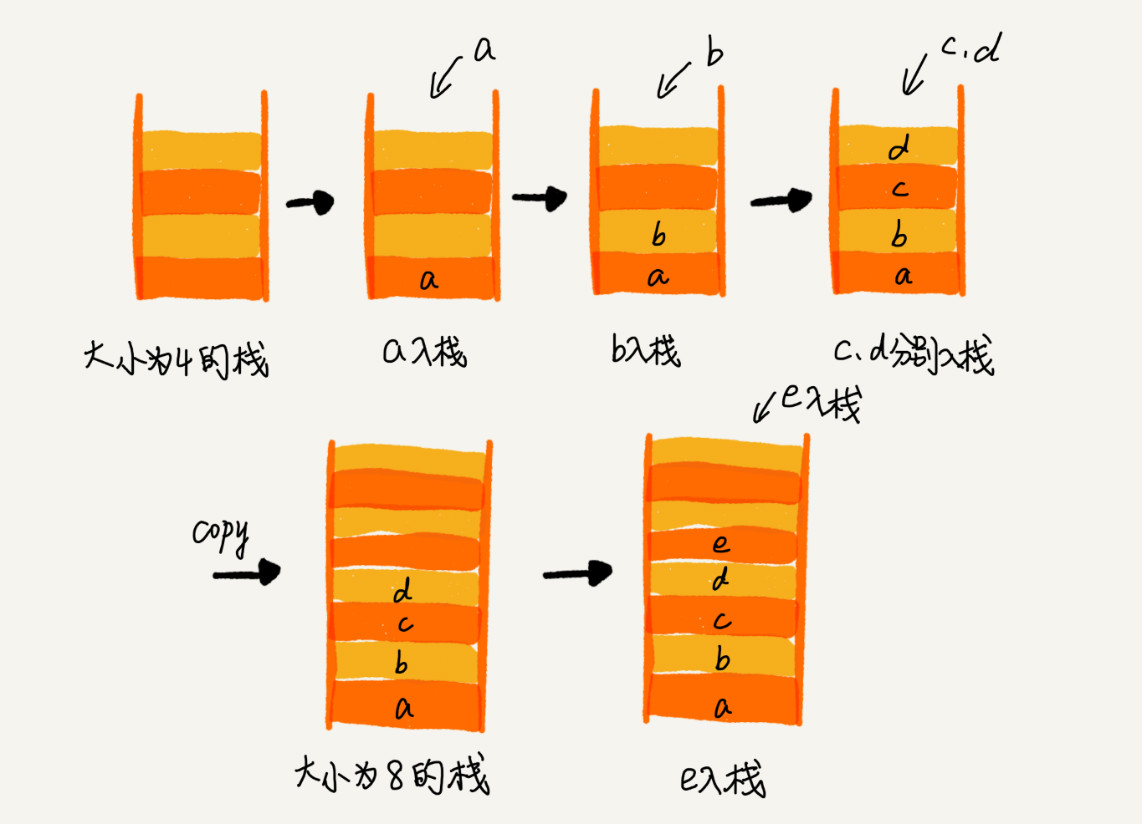

动态扩容的顺序栈，对于出栈操作来说，不会涉及到内存的重新申请和数据搬移，所以出栈的时间复杂度是O(1)。但是对于入栈操作来说，当栈中有空闲空间时，入栈操作的时间复杂度为O(1)，当空间不够时，就需要重新申请内存和数据搬移，时间复杂度就成了O(n)。
入栈操作，最好情况时间复杂度是O(1)，最坏情况时间复杂度是O(n)。均摊时时间复杂度是O(1)。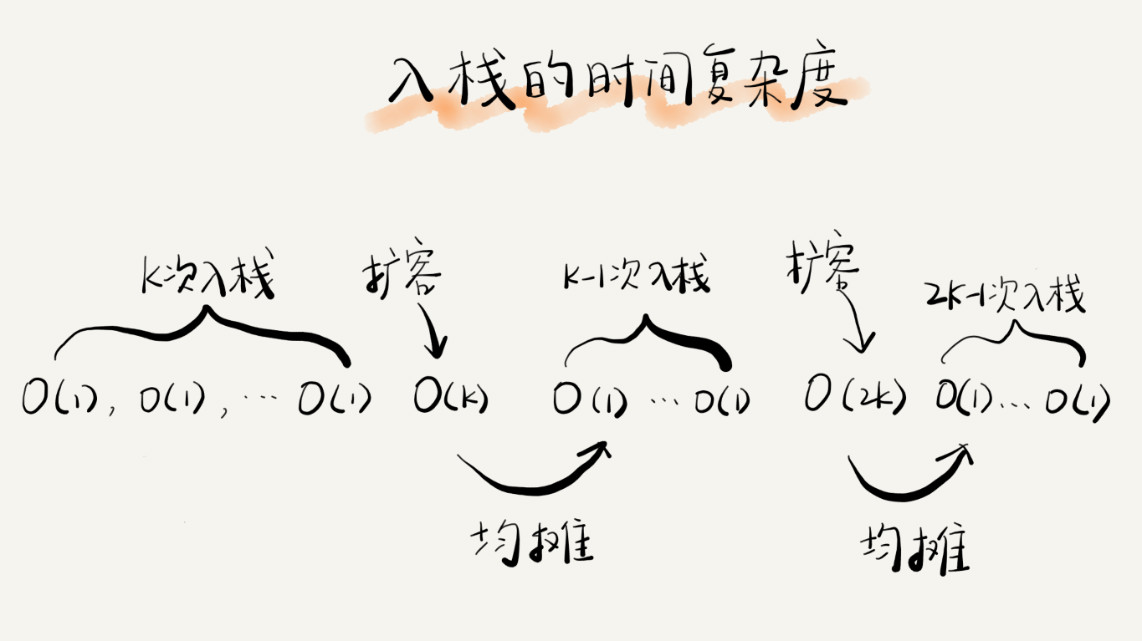

栈的应用

栈在函数调用中的应用

栈作为一个比较基础的数据结构，比较经典的一个应用场景是函数调用栈。
操作系统给每个线程分配了一块独立的内存空间，这块内存被组织成“栈”这种结构，用来存储函数调用时的临时变量。每进入一个函数，就会将临时变量作为一个栈帧入栈，当被调用函数执行完成，返回之后，将这个函数对应的栈帧出栈。

int main() {
   int a = 1; 
   int ret = 0;
   int res = 0;
   ret = add(3, 5);
   res = a + ret;
   printf("%d", res);
   reuturn 0;
}

int add(int x, int y) {
   int sum = 0;
   sum = x + y;
   return sum;
}

从代码中可以看出，main()函数调用了add()函数，获取计算结果，与临时变量a相加，最后打印res的值。下图可以看到这个过程对应的函数栈里出栈、入栈的操作，在执行到add()函数时，函数调用栈的情况。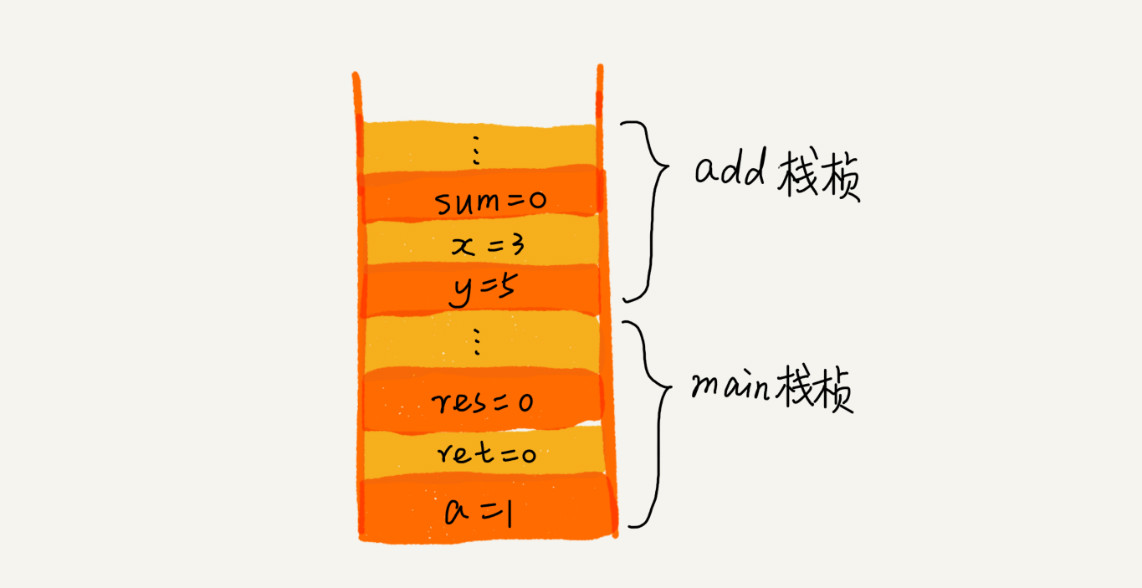

栈在表达式求值中的应用

栈的另一个常见的应用场景，编译器利用栈来实现表达式求值。
这里将算术表达式简化为只包含加减乘除四则运算(其实更复杂的还有与或非等逻辑运算、括号等)，比如：34+13*9+44-12/3。

对于这个四则运算，人脑可以很快求解出答案，但是对于计算机来说，理解这个表达式本身就是个挺难的事。

实际上，编译器就是通过两个栈来实现的。其中一个保存操作数的栈，另一个是保存运算符的栈。
从左向右遍历表达式，当遇到数字，直接压入操作数栈；当遇到运算符，就与运算符栈的栈顶元素比较。如果比运算符栈栈顶元素的优先级高，就将当前运算符压入栈；如果比运算符栈栈顶元素的优先级低或者相同，从运算符栈中取栈顶运算符，从操作数栈的栈顶取两个操作数，然后进行计算，再把计算完的结果压入操作数栈，继续比较。

如下图为 3+5*8-6 这个表达式的计算过程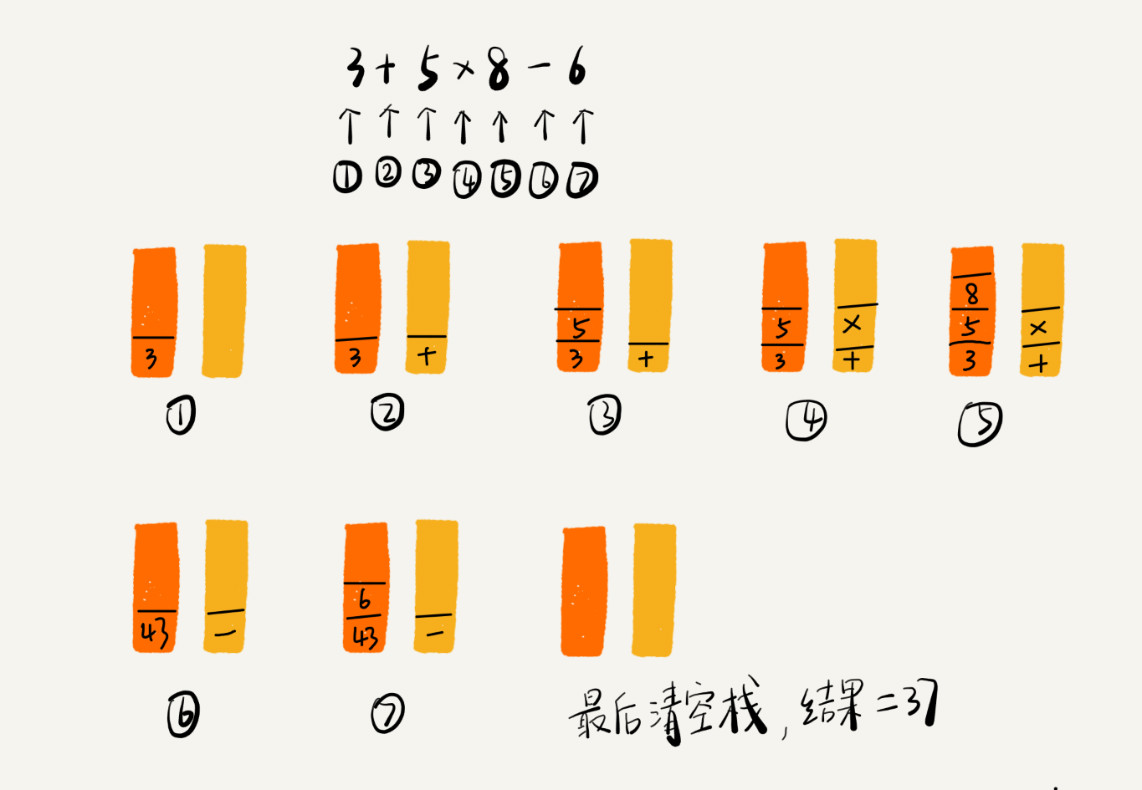

栈在括号匹配中的应用

借助栈来检查表达式中的括号是否匹配。

假设表达式中只包含三种括号，圆括号()、方括号[]、花括号{}，并且它们可以任意嵌套。
比如，{[()]}或[({})([])]等都为合法形式，而([){}]为不合法形式。
对于一个只包含括号的表达式字符串，如何检查它是否合法呢？

思路：用栈来保存未匹配的左括号，从左到右依次扫描字符串。当扫描到左括号时，就将其压入栈中；当扫描到右括号时，将其与栈顶左括号匹配，若能够匹配，将此栈顶左括号出栈，继续扫描其余的字符串。如果扫描过程中，遇到不能配对的右括号，或者栈中没有左括号，则说明为非法格式。当所有的括号都扫描完成之后，如果栈为空，则说明字符串为合法形式；否则，说明有未匹配的左括号，为非法格式。

class Solution {
    public boolean isValid(String s) {
        // 栈中只进左括号 每当有一个括号要进栈时就看它是不是与栈顶括号相匹配 匹配就pop 不匹配就进栈

        HashMap<Character, Character> map = new HashMap<>() {{
            put('(', ')');
            put('[', ']');
            put('{', '}');
        }};

        // Deque<Character> stack = new ArrayDeque<>();
        Deque<Character> stack = new LinkedList<>();
        for (int i = 0; i < s.length(); i ++) {
            char c = s.charAt(i);
            if (map.containsKey(c)) {
                // 左括号入栈
                stack.push(c);
            } else {
                if (stack.size() > 0 && map.get(stack.peek()).equals(c)) {
                    // 栈不为空，并且左右括号匹配  出栈
                    stack.pop();
                } else {
                    return false;
                }
            }
        }
        return stack.size() == 0;
    }
}

思考

用两个栈来实现浏览器的前进、后退功能

使用两个栈X和Y，把首次浏览的页面依次压入栈X。
当点击后退按钮时，依次从栈X中出栈，并将出栈的数据依次放入栈Y。当点击前进按钮时，依次从栈Y中取出数据，放入栈X中。
当栈X中没有数据时，就说明没有页面可以继续后退浏览了。当栈Y中没有数据，说明没有页面可以点击前进按钮浏览了。

举个例子，我们顺序查看了a-b-c三个页面，依次把a、b、c压入栈：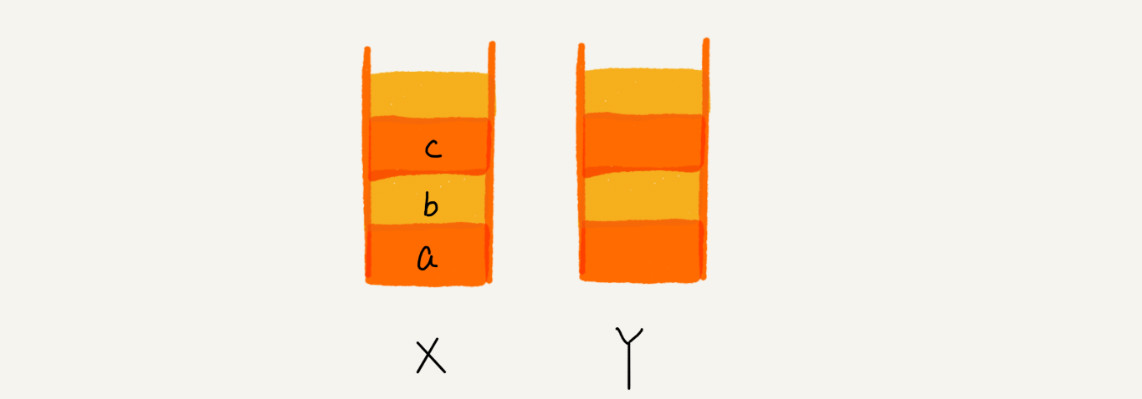

通过浏览器的后退按钮，从页面c后退到页面a之后，就依次把c和b从栈X中弹出，并且依次放入到栈Y中：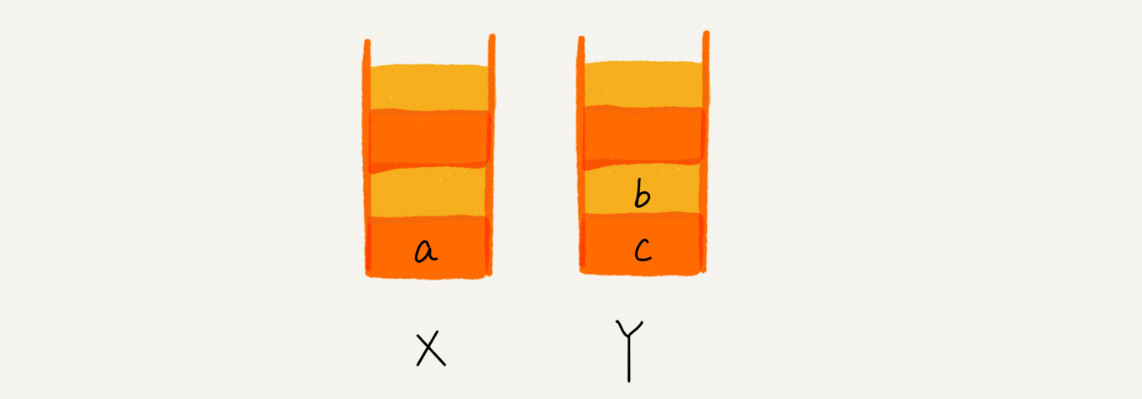

点击前进按钮回到b页面，将b从栈Y中弹出，放入栈X：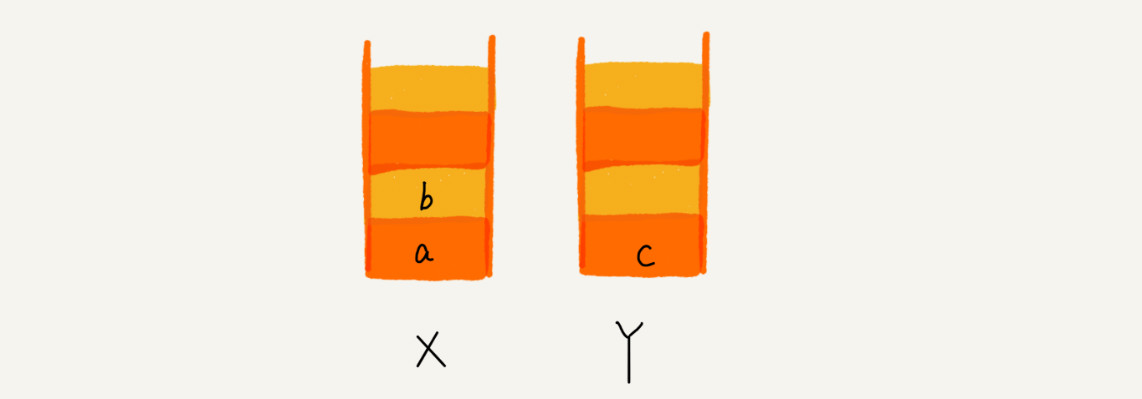

通过页面b跳转到新的页面d，页面c就无法再通过前进、后退按钮重复查看，这时清空栈Y：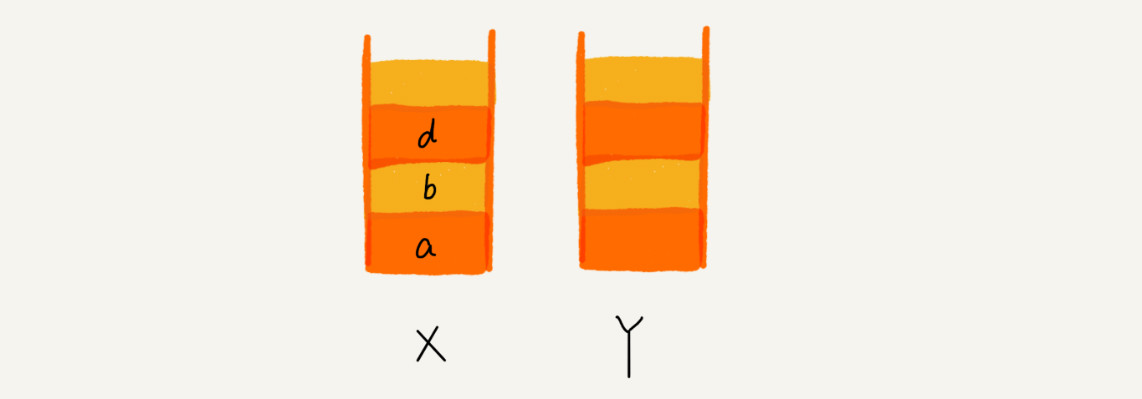

为什么函数调用要用“栈”来保存临时变量？用其他数据结构不行吗?

不一定非要用栈来保存临时变量，只不过如果这个函数调用符合后进先出的特性，用栈这种数据结构来实现，是最好的选择。
从调用函数进入被调用函数，对于数据来说，变化的是作用域。所以根本上，只要能保证每进入一个新的函数，都是一个新的作用域就可以。而要实现这个，用栈就非常方便。在进入被调用函数的时候，分配一段栈空间给这个函数的变量，在函数结束的时候，将栈顶复位，正好回到调用函数的作用域内。

JVM的虚拟机栈 VS 数据结构的栈

JVM内存管理中有个“堆栈”的概念。栈内存用来存储局部变量和方法调用，堆内存用来存储java中的对象。那JVM中的“栈”和这里说的“栈”是不是一回事？如果不是，那它为什么又叫做“栈”?
内存中的栈和数据结构的栈不是一个概念。
内存中的堆栈是内存中的数据区域，是一段虚拟的内存空间；数据结构中的堆栈是抽象的数据存储结构。但是它们都有“栈”的特性。

内存空间在逻辑上分为三部分：代码区、静态数据区和动态数据区，动态数据区又分为堆和栈。
代码区：存储方法体的二进制代码。高级调度(作业)、中级调度(内存)、低级调度(进程)控制代码区执行代码的切换。
静态数据区：存储全局变量、静态变量、常量，常量包括final修饰的常量和String常量。系统自动分配和回收。
栈区：存储运行方法的形参、局部变量、返回值。由系统自动分配和回收。
堆区：new一个对象的引用或地址存储在栈区，指向该对象存储在堆区中的真实数据。