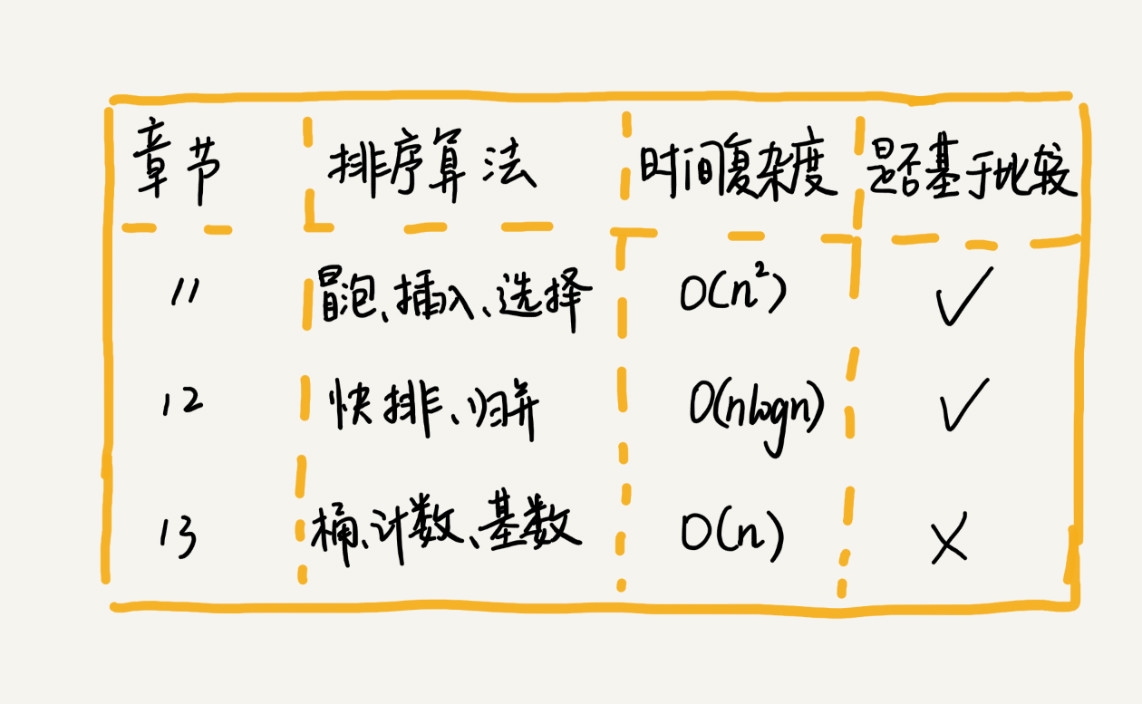
一、排序(上)：为什么插入排序比冒泡排序更受欢迎？

分析一个排序算法，从哪几方面入手：

1.排序算法的执行效率

1）最好情况、最坏情况、平均情况时间复杂度。
2）时间复杂度的系数、常数、低阶。
3）比较次数和交换(或移动)次数。基于比较的排序算法会涉及两种操作，一种是元素比较大小，另一种是元素交换或移动。

2.排序算法的内存消耗

算法的内存消耗可以通过空间复杂度来衡量，针对排序算法的空间复杂度，引入了一个概念——原地排序(Sorted in place)。原地排序算法就是特指空间复杂度为O(1)的排序算法，包括冒泡排序、插入排序、选择排序。

3.排序算法的稳定性

除了执行效率和内存消耗，针对排序算法还有一个重要的度量指标——稳定性。这个概念是说，如果待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序不变。
假如现在有一组数据：2，9，3，4，8，3，按照大小排序之后是2，3，3，4，8，9。这组数据里有两个3，经过某种排序算法排序之后，如果两个3的前后顺序没有改变，那这种排序算法就是稳定的排序算法；如果前后顺序发生变化，那对应的排序算法就是不稳定的。
数据结构和算法在讲排序的时候，都是用整数来举例，在真正软件开发中，要排序的往往不是单纯的整数，而是一组对象，需要按照对象的某个key来排序。
比如，现在要给电商交易系统中的“订单”排序，订单有两个属性，一个是下单时间，另一个是订单金额。如果现在有10万条订单数据，希望按照金额从小到大对订单数据排序。对于金额相同的订单，希望按照下单时间从早到晚有序。
对于这样一个排序需求，借助稳定排序算法，先按照下单时间给订单排序，然后用稳定排序算法，按照订单金额重新排序。这样两遍排序之后，得到的订单数据就是按照金额从小到大排序，金额相同的订单按照下单时间排序。稳定排序算法可以保持金额相同的两个对象，在排序之后的前后顺序不变。

1.冒泡排序

1.1冒泡排序是原地排序算法吗？

冒泡的过程只涉及相邻数据的交换操作，只需要常量级的临时空间，所以它的空间复杂度为O(1)，是一个原地排序算法。

1.2冒泡排序是稳定的排序算法吗？

在冒泡排序中，只有交换才可以改变两个元素的前后顺序。为了保证冒泡排序算法的稳定性，当有相邻的两个元素大小相等的时候，不做交换，相同大小的数据在排序前后不会改变顺序，所以冒泡排序是稳定的。

1.3冒泡排序的时间复杂度

最好情况下要排序的数据是有序的，只需要进行一次比较操作，是O(n)。而最坏情况下，要排序的数据刚好是倒序排列的，要进行n次冒泡操作，为O(n2)。
对于包含n个数据的数组，这n个数据有n!中排列方式。不同的排列方式，冒泡排序执行的时间肯定是不同的，如果用概率论方法定量分析平均时间复杂度，涉及的数学推理和计算很复杂。
这里，通过“有序度”和“逆序度”这两个概念来进行分析。
有序度是数组中具有有序关系的元素对的个数。

1
有序元素对：a[i] <= a[j], 如果 i < j。


对于一个倒序排列的数组，比如654321，有序度为0；对于一个完全有序的数组，比如123456，有序度就是n×(n-1)/2，就是15。我们把这种完全有序的数组的有序度叫做满有序度。
逆序度的定义正好跟有序度相反(默认从小到大为有序)。

逆序度 = 满有序度 - 有序度

排序的过程就是增加有序度，减少逆序度的过程，最后达到满有序度。

对于包含n个数据的数组进行冒泡排序，平均交换次数在最坏情况下，初始状态有序度为0，要进行n×(n-1)/2次交换；最好情况下，初始状态的有序度是n×(n-1)/2，就不需要进行交换。取中间值n×(n-1)/4来表示平均情况。定性分析下平均情况的时间复杂度为O(n2)。

2.插入排序

2.1插入排序是原地排序算法吗？

插入排序算法不需要额外的存储空间，所以空间复杂度是O(1)，也就是说，这是一个原地排序算法。

2.2插入排序是稳定的排序算法吗？

在插入排序中，对于值相同的元素，可以选择将后面出现的元素，插入到前面出现元素的后面，这样就可以保持原有的前后顺序不变，所以插入排序是稳定的排序算法。

2.3插入排序的时间复杂度

最好情况下从头遍历已经有序的元素O(n)；最坏情况下数组是倒序的，每次插入都相当于在数组的第一个位置插入新的数据，为O(n2)。平均时间复杂度为O(n2)。

3.选择排序

选择排序算法的实现思路有点类似插入排序，也区分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾。

3.1选择排序是原地排序算法吗？

空间复杂度为O(1)，是一种原地排序算法。

3.2选择排序是稳定的排序算法吗？

选择排序是一种不稳定的排序算法。

3.3选择排序的时间复杂度

选择排序的最好情况时间复杂度、最坏情况和平均情况时间复杂度都为O(n2)。

为什么插入排序要比冒泡排序更受欢迎？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
冒泡排序中数据的交换操作：
if (a[j] > a[j+1]) { // 交换
   int tmp = a[j];
   a[j] = a[j+1];
   a[j+1] = tmp;
   flag = true;
}

插入排序中数据的移动操作：
if (a[j] > value) {
  a[j+1] = a[j];  // 数据移动
} else {
  break;
}

从代码实现上看，冒泡排序的数据交换要比插入排序的数据移动操作要多，cpu处理时间就长。虽然两者时间复杂度一样，但是插入排序优化空间要大，例如其中的希尔排序。

二、排序(下)：如何用快排思想在O(n)内查找无序数组中第k大元素？

时间复杂度为O(nlogn)的归并排序和快速排序，都用到了分治思想。

4.归并排序(Merge Sort)

思想：要排序一个数组，先把数组从中间分成前后两部分，然后对前后两部分分别排序，再将排好序的两部分合并在一起，这样整个数组就都有序了。
归并排序使用的是分治思想。

1
2
3
4
5
//归并排序的递推公式
递推公式：
merge_sort(p…r) = merge(merge_sort(p…q), merge_sort(q+1…r))
终止条件：
p >= r 不用再继续分解

给下标从p到r的数组排序，将这个排序问题转化为两个子问题，p到q和q+1到r，下标q等于p和r的中间位置(p+r)/2。当两个子数组都排好序之后，合并在一起，p到r也就排好序了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
// 归并排序算法, A 是数组，n 表示数组大小
merge_sort(A, n) {
  merge_sort_c(A, 0, n-1)
}

// 递归调用函数
merge_sort_c(A, p, r) {
  // 递归终止条件
  if p >= r  then return

  // 取 p 到 r 之间的中间位置 q
  q = (p+r) / 2
  // 分治递归
  merge_sort_c(A, p, q)
  merge_sort_c(A, q+1, r)
  // 将 A[p...q] 和 A[q+1...r] 合并为 A[p...r]
  merge(A[p...r], A[p...q], A[q+1...r])
}

merge(A[p...r], A[p...q], A[q+1...r]) {
  var i := p，j := q+1，k := 0 // 初始化变量 i, j, k
  var tmp := new array[0...r-p] // 申请一个大小跟 A[p...r] 一样的临时数组
  while i<=q AND j<=r do {
    if A[i] <= A[j] {
      tmp[k++] = A[i++] // i++ 等于 i:=i+1
    } else {
      tmp[k++] = A[j++]
    }
  }
  
  // 判断哪个子数组中有剩余的数据
  var start := i，end := q
  if j<=r then start := j, end:=r
  
  // 将剩余的数据拷贝到临时数组 tmp
  while start <= end do {
    tmp[k++] = A[start++]
  }
  
  // 将 tmp 中的数组拷贝回 A[p...r]
  for i:=0 to r-p do {
    A[p+i] = tmp[i]
  }
}

4.1归并排序是稳定的排序算法吗？

归并排序的稳定性要看merge()合并函数。另外，稳定性是由方法本身决定的，对不稳定的排序方法而言，不管其描述形式如何，总能举出一个说明不稳定的实例来；反之，对稳定的排序方法，总能找到一种不引起不稳定的描述形式。
合并前后的前后顺序不变，就是稳定的。

4.2归并排序的时间复杂度

归并排序可以递归实现，递归代码的时间复杂度也可以写成递推公式。
我们假设对 n 个元素进行归并排序需要的时间是 T(n)，那分解成两个子数组排序的时间都是 T(n/2)。merge() 函数合并两个有序子数组的时间复杂度是 O(n）。

1
2
3
4
5
6
7
8
9
10
T(1) = C；   n=1 时，只需要常量级的执行时间，所以表示为 C。
T(n) = 2*T(n/2) + n； n>1

T(n) = 2*T(n/2) + n
     = 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2*n
     = 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n
     = 8*(2*T(n/16) + n/8) + 3*n = 16*T(n/16) + 4*n
     ......
     = 2^k * T(n/2^k) + k * n
     ......

当T(n/2^k)=T(1)时，也就是n/2^k=1，得到k=log2n。代入得到T(n)=Cn+nlog2n。大O标记法表示就是T(n)=O(nlogn)。

4.3归并排序的空间复杂度

归并排序的时间复杂度任何情况下都是O(nlogn)，但是归并排序并没有像快排那样应用广泛，原因在于它不是原地排序算法。因为归并排序的合并函数，在合并两个有序数组为一个有序数组时，需要借助额外的存储空间。
空间复杂度为O(n)。

5.快速排序(Quick Sort)

快排利用的也是分治。不稳定。
思想：假设要排序数组中下标从p到r之间的一组数据，我们选择p到r之间的任意一个数据作为pivot(分区点)。遍历p到r之间的数据，将小于pivot的放到左边，将大于pivot的放到右边，将pivot放到中间。经过这一步骤之后，数组p到r之间的数据就被分成了三个部分，前面p到q-1之间都是小于pivot的，中间是pivot，后面的q+1到r之间是大于pivot的。
根据分治、递推的处理思想，递归排序下标从p到
q-1之间的数据和下标从q+1到r之间的数据，直到区间缩小为1，说明所有的数据都有序了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
递推公式：
quick_sort(p…r) = quick_sort(p…q-1) + quick_sort(q+1, r)

终止条件：
p >= r

// 快速排序，A 是数组，n 表示数组的大小
quick_sort(A, n) {
  quick_sort_c(A, 0, n-1)
}
// 快速排序递归函数，p,r 为下标
quick_sort_c(A, p, r) {
  if p >= r then return
  
  q = partition(A, p, r) // 获取分区点
  quick_sort_c(A, p, q-1)
  quick_sort_c(A, q+1, r)
}

归并排序的处理过程是从下到上的，先处理子问题，然后再合并。而快排正好相反，它的处理过程由上到下，先分区，然后再处理子问题。快排通过设计巧妙的原地分区函数，可以实现原地排序，解决了归并排序占用太多内存的问题。

思考题

现在有10个接口访问日志文件，每个日志文件大小约为300MB，每个文件里的日志都是按照时间戳从小到大排序的。希望将这10个较小的日志文件，合并为1个日志文件，合并之后的日志仍然按照时间戳从小到大排列。如果处理上述排序任务的机器内存只有1GB，如何能“快速”地将这10个日志文件合并？

三、线性排序：如何根据年龄给100万用户数据排序？

桶排序、计数排序、基数排序，这三种排序算法的时间复杂度是线性的，所以叫做线性排序(Linear Sort)。之所以能做到线性的时间复杂度，是因为这三个算法是非基于比较的排序算法，都不涉及元素之间的比较操作。

6.桶排序

核心思想是将要排序的数据分到几个有序的桶里，每个桶里的数据再单独进行排序。桶内排完序之后，再把每个桶里的数据按照顺序依次取出，组成的序列就是有序的了。

6.1桶排序的时间复杂度

如果要排序的数据有n个，我们把它们均匀地划分到m个桶内，每个桶内就有k=n/m个元素。每个桶内部使用快速排序，时间复杂度为O(klogk)。m个桶排序的时间复杂度就是O(mklogk)，因为k=n/m，所以整个桶排序的时间复杂度就是O(nlog(n/m))。当桶的个数m接近数据个数n时，log(n/m)就是一个非常小的常量，这个时候桶排序的时间复杂度接近O(n)。

6.2桶排序的应用场景

桶排序对要排序数据的要求非常苛刻。首先，要排序的数据需要很容易就能划分成m个桶，并且，桶与桶之间有着天然的大小顺序。这样每个桶内的数据排序完之后，桶与桶之间的数据不需要在进行排序。其次，数据在各个桶之间的分布是比较均匀的，如果数据经过桶的划分，有些桶里的数据非常多，有些非常少，很不平均，那桶内数据排序的时间复杂度就不是常量级了，在极端情况下，如果数据都被分到一个桶里，那就退化为O(nlogn)了。
桶排序比较适合用在外部排序中。所谓的外部排序就是数据存储在外部磁盘中，数据量比较大，内存有限，无法将数据全部加载到内存中。
比如说我们有10GB的订单数据，希望按订单金额(假设金额都是正整数)进行排序，但是我们内存有限，只有几百MB，没办法一次性把10GB的数据都加载到内存中。这个时候可以借助桶排序的思想来解决这个问题。

7.计数排序(Counting Sort)

计数排序可以说是桶排序的一种特殊情况。
当要排序的n个数据，所处的范围并不大的时候，比如最大值是k，我们就可以把数据划分成k个桶。每个桶内的数据值都是相同的，省掉了桶内排序的时间。
我们都经历过高考，高考查分系统，我们查分数的时候，系统会显示我们的成绩以及所在省的排名。2016年山东省有70万考生，如何通过成绩快速排序得出名次呢？
考生的满分是750分，最小是0分，这个数据的范围不算大，所以我们可以分成751个桶，对应分数从0到750分。根据考生的成绩，将这70万考生划分到751个桶里。桶内的数据都是分数相同的考生，所以并不需要再进行排序。只需要依次扫描每个桶，将桶内的考生依次输出到一个数组中，就实现了70万考生的排序，因为只涉及扫描遍历操作，所以时间复杂度是O(n)。
计数排序的算法思想与桶排序类似，只是桶的大小粒度不一样，为什么叫“计数”，“计数”的含义来自哪里？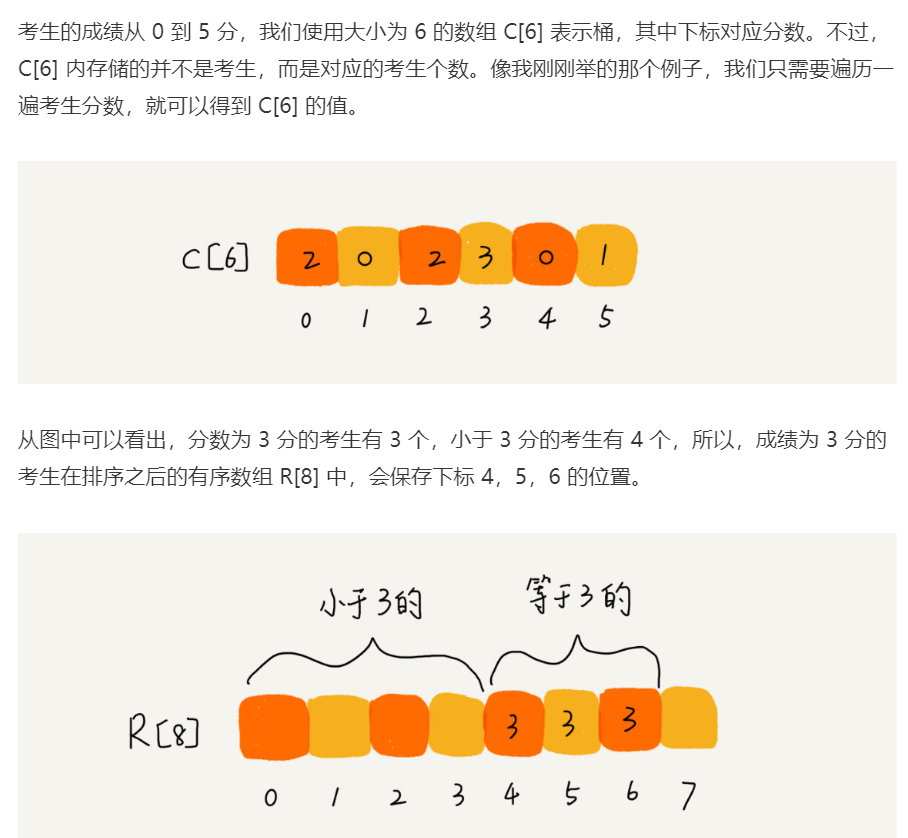



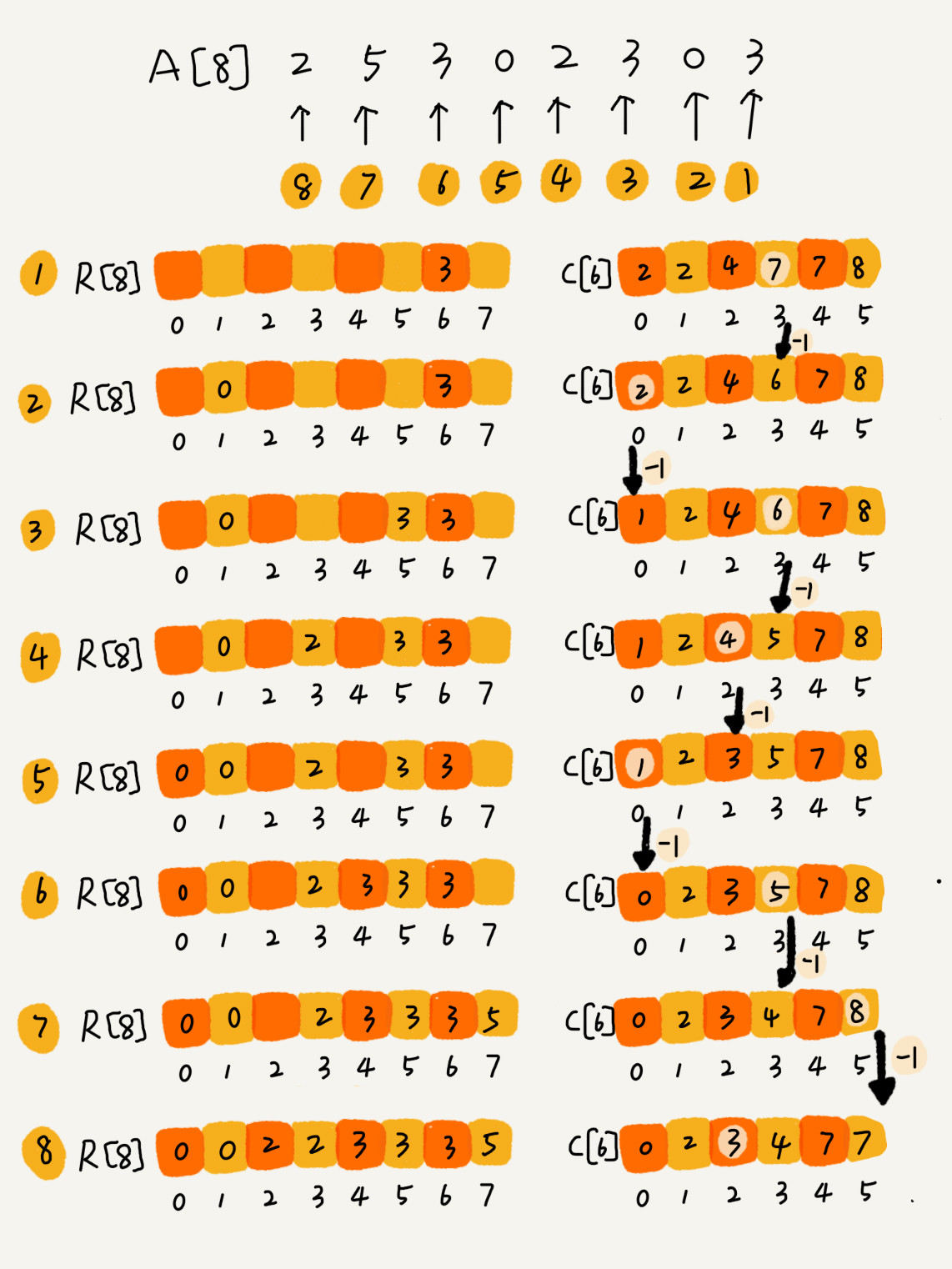
8.基数排序(Radix Sort)

再来看这样一个排序问题，假设我们有10万个手机号码，希望将这10万个手机号码从小到大排序，有什么比较快速的排序方法？
快排可以做到O(nlogn)，手机号码有11位，范围太大，不适合用桶排序、计数排序。
可以用基数排序。
假设要比较两个手机号码a和b的大小，如果在前面几位中，a手机号码已经比b的大了，那后面的几位就不用看了。
基数排序是一种借助多关键字排序的思想对单逻辑关键字进行排序的方法。