优先队列的作用是能保证每次取出的元素都是队列中权值最小的(Java的优先队列每次取最小元素，C++的优先队列每次取最大元素)。
这里牵涉到了大小关系，元素大小的评判可以通过元素本身的自然顺序(natural ordering)，也可以通过构造时传入的比较器(Comparator，类似于C++的仿函数)。

Java中PriorityQueue实现了Queue接口，不允许放入null元素。
其通过堆实现，具体说是通过**完全二叉树(complete binary tree)实现的小顶堆(任意一个非叶子节点的权值，都不大于其左右子节点的权值)**，也就意味着可以通过数组来作为PriorityQueue的底层实现。

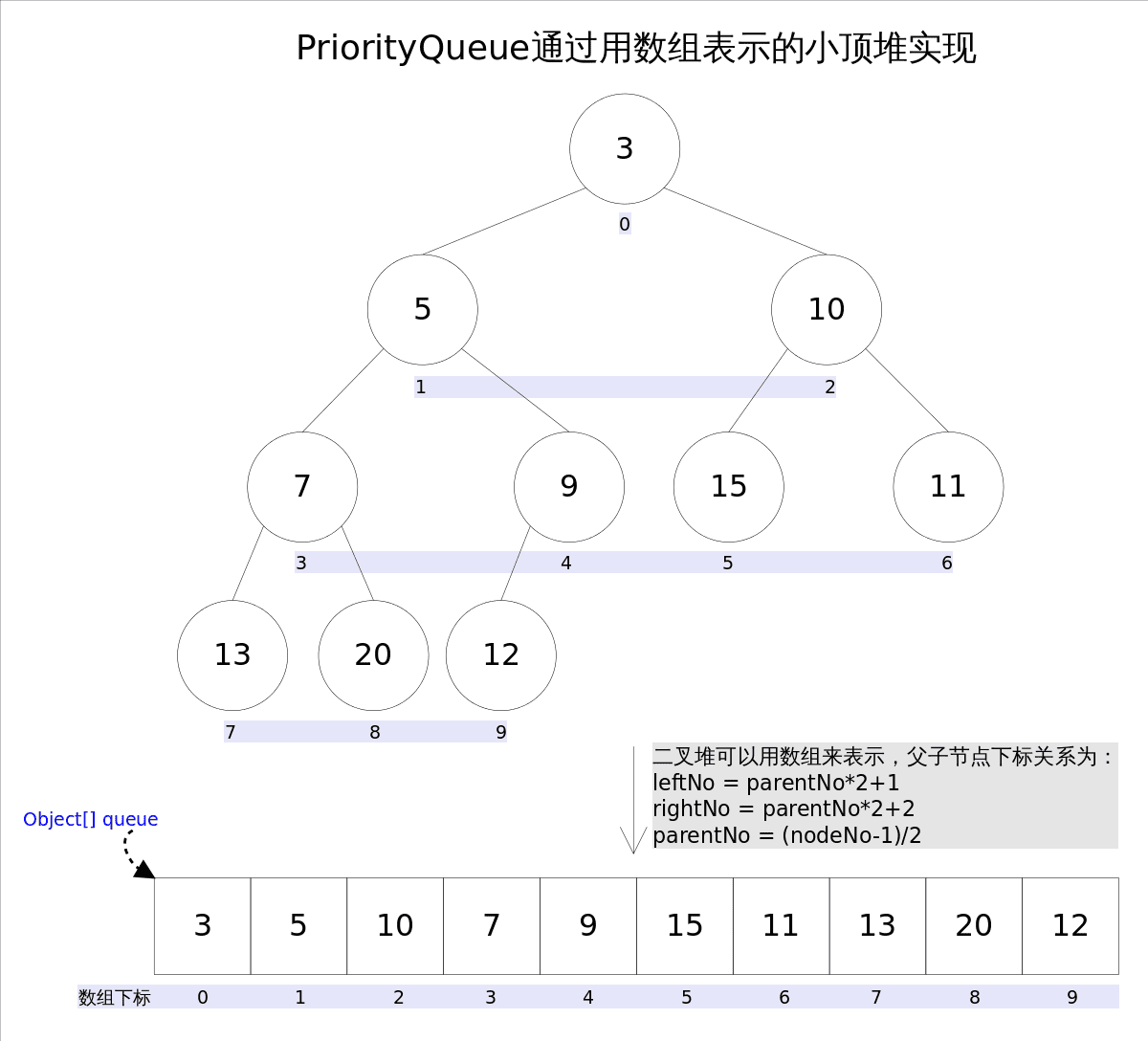
父子节点的编号之间有如下关系：

  1. leftNo = parentNo*2+1
  2. rightNo = parentNo*2+2
  3. parentNo = (nodeNo-1)/2

通过上述三个公式，可以轻易计算出某个节点的父节点以及子节点的下标。
这也就是为什么可以直接用数组来存储堆的原因。

PriorityQueue的peek()和element()操作是常数时间；add()、offer()、无参数的remove()以及poll()方法的时间复杂度都是log(N)。

PriorityQueue方法剖析

add()和offer()

element()和peek()

remove()和poll()

remove(Object o)

top-K问题

给你100w个数据，设计一个算法找到你前10个最大的元素

  1. 思路一
    从小到大排序，再输出后10个元素，这虽然是一种解决方法，但面试官一般不会让你这样做，那样这个问题就没有意义了
  2. 思路二
    将这一百万个元素整体建成一个大根堆，再依次出队10个元素即可，但占用的内存是不是有点多呢？
  3. 最优解
    只建k个元素的小根堆，如果后续元素比堆顶元素大，那么先出队，然后再将这个元素入队，当遍历完整个数据时，最后小根堆上即为我们的top-k。

延伸问题：

  1. 求前k个最大元素，建一个k个元素的小根堆，如果后续元素比堆顶元素大，那么先出队，然后再将这个元素入队
  2. 求前k个最小元素，建一个k个元素的大根堆，如果后续元素比堆顶元素小，那么先出队，然后再将这个元素入队
  3. 求第k大的元素，建一个小堆，堆顶元素就是第k大的元素
  4. 求第k小的元素，建一个大堆，堆顶元素就是第k小的元素

代码实现：求数组中前K个最小的元素 - 大根堆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
public class TopK {
    /**
     * 求数组中前K个最小的元素
     * @param array
     * @param k
     * @return
     */
    public static int[] topk(int[] array ,int k){
        //1.创建一个大小为k的大根堆
        PriorityQueue<Integer> maxHeap = new PriorityQueue<>(k, new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2 - o1;
            }
        });
        //2.遍历数组中当中的元素，前k个元素放到队列中
        for (int i = 0; i < array.length; i++) {
            if (maxHeap.size() < k){
                maxHeap.offer(array[i]);
            }else {
                int top = maxHeap.peek();
                if (top > array[i]){
                    maxHeap.poll();
                    maxHeap.offer(array[i]);//将新元素放入其中
                }
            }
        }
        int[] ret = new int[k];
        for (int i = 0; i < k; i++) {
            ret[i] = maxHeap.poll();
        }
        return ret;
    }
    public static void main(String[] args) {
        int[] array = {18,21,8,10,34,21};
        int[] ret = topk(array, 3);
        System.out.println(Arrays.toString(ret));
    }
}